       |
||||||||||||||||||||||||||||||||||||||||||||||||||
| フェルマーの最終定理と未解決問題 ～解決までの歴史的潮流～ |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 埼玉県立蓮田高等学校 教職員研究会 2003年12月 執筆 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 目次 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| §１．\(\textrm{FLT}\,\)とは何か §２．解決当時の状況 §３．解決までの過程 §４．A.Wiles による解説 §５．未解決問題の例 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| §１．\(\textrm{FLT}\,\)とは何か | ||||||||||||||||||||||||||||||||||||||||||||||||||
| フェルマー (Pierre de Fermat, 1607-1665) が本の余白に書き遺した「フェルマーの最終定理 Fermat's Last Theorem \((\)\(\textrm{FLT}\)\()\)」とは, | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(n\,\)が\(\,3\,\)以上の整数のとき, \(\,x^{\!\:n}\!+y^{\!\:n}\!=z^{\!\:n}\,\)をみたす自然数の組\(\,(x,\,y,\,z)\,\)は存在しない | ||||||||||||||||||||||||||||||||||||||||||||||||||
| という命題を指す. フェルマーは, 南フランスのトゥールーズで裁判官や議会の勅選委員を職務とする傍ら, 数学研究に対して並々ならぬ情熱を注いだ. 彼は, ディオファントス (Diophantus, ３世紀頃) の数学書『算術』を読み進める中で, 新たな命題を独自に発見すると, その本の余白に (証明を記すことなく) その命題のみを書き込んだという. 彼の死後, その本から48種類もの書き込みが発見され, やがて世に知られるようになる. 後に他の多くの数学者たちによって個々にその真偽が検証されていったが, 上の命題だけは解決されないまま長い年月が過ぎていったのである. \(\textrm{FLT}\,\)において\(\,n\!=\!2\,\)とすると,「ピタゴラスの定理」として知られる等式\[\textcolor{blue}{x^{\!\:2}\!+y^{\!\:2}\!=z^{\!\:2}}\] が現れる. この等式をみたす原始ピタゴラス数は, \[(x,\,y,\,z)=(3,\,4,\,5),\:(5,\,12,\,13),\:(8,\,15,\,17),\:\cdots\cdots\] など, 無数に存在する. しかし, 指数\(\,n\,\)が\(\,3\,\)以上の場合, すなわち, \[\begin{equation}\begin{split}&x^{\!\:3}\!+y^{\!\:3}\!=z^{\!\:3}\\ &x^{\!\:4}\!+y^{\!\:4}\!=z^{\!\:4}\\ &x^{\!\:5}\!+y^{\!\:5}\!=z^{\!\:5}\\ &\:\:\cdots\cdots\\ &x^{\!\:n}\!+y^{\!\:n}\!=z^{\!\:n}\\ &\:\:\cdots\cdots\end{split}\end{equation}\tag{1.1}\]のような等式については, \(\,x,\,y,\,z\,\)にいかなる自然数を代入しても成立しない, とフェルマーは主張したのである. この主張を (証明を記すことなく) 書き込んだ後, フェルマーは続けて「この命題について真に驚くべき証明を発見したが, それを書くにはこの余白は狭すぎる」と付け加えた. ところが彼は,『算術』読了後もしばらく生存していたにも拘らず, その「真に驚くべき証明」をどこにも書き遺さなかった. その生涯において多くの優れた数学的業績を挙げ, 他の命題に関しては折に触れて証明の方針を示していたことに鑑みると, 彼は, その「驚くべき証明」が勘違いであったことに後になって気づいたのではないか. 数学の世界では, 証明された命題を「定理」といい, 証明されてはいないが様々な事象から正しいと考えられる命題を「予想」という. 上の命題は, 長い間「フェルマー予想」と呼ばれていた. ところが, その後の数学の発展により,「証明されてはいないが真である可能性が高い」と多くの専門家から信じられるようになっていった. フェルマーが本の余白に書き込んだ他の命題はすべて解決 (証明) されたにも拘らず, この命題だけが最後まで残されたため, 幻の「証明を発見した」フェルマーへの敬意を込めて「\(\textrm{FLT}\)」と呼ばれるようになったのであろう. |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| フェルマー自身が「証明した」としても, 肝心の「証明」が現存しないのであるから, 我々にとってはこの命題の真偽は不明のままである. フェルマーの主張を覆すような「反例」すなわち「等式\(\,(1.1)\,\)が成り立つような自然数の組\(\,(x,\,y,\,z)\,\)」が一つでも発見されれば, この命題は「偽」と判定される. 逆に, この命題が「真」であることを「証明」するためには, \(\,3\,\)以上のすべての指数\(\,n\,\)について, どのような自然数\(\,x,\,y,\,z\,\)を代入しても等式\(\,(1.1)\,\)が成立しないことを示さなければならない. 試みに, 反例を探してみよう. まずは\(\,n\!=\!3\,\)の場合, すなわち\[x^{\!\:3}\!+y^{\!\:3}\!=z^{\!\:3}\] をみたす\(\,x,\,y,\,z\,\)を探すことから始めることになる. たとえば, 私がいま思いついた適当な自然数を\(\,x,\,y,\,z\,\)に代入することで得た |
||||||||||||||||||||||||||||||||||||||||||||||||||
| \(5^{\!\:3}\!+8^{\!\:3}\!=9^{\!\:3}\) \(292^{\!\:3}\!+371^{\!\:3}\!=419^{\!\:3}\) \(1140^{\!\:3}\!+1387^{\!\:3}\!=1607^{\!\:3}\) |
||||||||||||||||||||||||||||||||||||||||||||||||||
| などはいかがであろうか. 計算してみれば分かるように, これらの「等式」はいずれも成立していない. さて, 上の例では反例探しに失敗したが, 諦めるのはまだ早い. 私が思いつきで代入した数値が適切でなかっただけかも知れない. 幸い, \(\,x,\,y,\,z\,\)に代入しうる数値の組み合わせは他にも無数にある. これらを一つ一つシラミ潰し的に代入して計算していけば, いつかは反例となる等式を発見できるかも知れない. しかし, 無数の組み合わせをもつ\(\,x,\,y,\,z\,\)に個別に数値を代入して調べるとなると, 反例を発見するまでに (コンピューターを援用したとしても) 膨大な時間を (発見できなければ無限の時間を) 要することになる. \(n\!=\!3\,\)の場合に反例を発見できなければ, 次に\(\,n\!=\!4\,\)の場合について同様の作業を始めることになるが, それでも発見できなければ, \(\,n\!=\!5,\,6,\,7,\,\cdots,\,99,\,100,\,\cdots\,\) のように値をひとつずつ増やして, 同様の数値計算を繰り返すことになる. 後の時代の各国の数学者たちは, \(\,\textrm{FLT}\,\)の反例あるいは証明を得ようと懸命に研究したが, 最終的な解決を得られずにいた. この問題が世に知られるようになって240年以上経過しても未解決であったことから, 20世紀初頭には, 高額な懸賞金制度まで設けられた. これは, 多くの数学愛好家たちをも奮闘させることになる. 実際, これまでに多くのアマチュアたちからも「証明」論文が次々と提出されたが, 結果としては, それらにはすべて何らかの誤謬が含まれていたのであった. 多くの数学者や数学愛好家たちの努力にも拘らず, 最新コンピューターを駆使して「反例」を探す作業も含め, 未解決で終わったのである. 数学の世界では,「大体は正しい」は通用しない. 論理に一分の隙もない状態で論証できなければ, 数学 (証明) としては無意味である. アマチュアの論文はともかくとして, プロの数学者の論文であっても, 査読者 (同一分野の研究者たち) から僅かな論理の隙を指摘され, 全体として無意味な論文と判定されることも (\(\,\textrm{FLT}\,\)の証明に関しては) 多く見受けられた現象であった. 一方, そのような試行錯誤を繰り返す中で, 多くの数学者たちが\(\,\textrm{FLT}\,\)解決に必要な道具 (概念や理論) を次々と創造しつつ数学を高度に発展させてきたという長い歴史がある. 数学者は, 新たな数学を構築するのに有用となる命題を, 価値のある「定理」と見なす. 逆に, 有用でないものは, (たとえそれが「真」であるにせよ) 数学的には無価値と見なされる. 残念ながら, \(\,\textrm{FLT}\,\)には, それを根拠として新たな理論を構築しうるだけの有用性がなく, その意味では\(\,\textrm{FLT}\,\)自体に「定理」としての価値はない. しかし, 数論をはじめ, 代数や解析など, \(\,\textrm{FLT}\,\)解決を目指した研究によって複数分野にわたる数学理論を目覚ましく進展させてきた歴史に鑑みれば, \(\,\textrm{FLT}\,\)には無視できぬ存在価値があったと言えよう. \(\textrm{FLT}\,\)の最終的な解決は, 1995年に, プリンストン大学教授のワイルズ (Andrew Wiles, 1953- ) によってもたらされた. その証明方法は, 多くの著名数学者たちの長年の研究によって構築された最先端の数学理論を駆使した「真に驚くべき証明」であった. それは, いかに優秀なフェルマーといえども, 単独で考案しうるようなレヴェルのものではなかった. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| §２．解決当時の状況 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\textrm{FLT}\,\)が公にされてから320年以上もの時を経て, 10年ほど前にようやくこの問題が解決されたというニュースが世界中に報道された.
解決が発表された瞬間の様子を伝えた栗原将人氏 (東京都立大学) のレポートを,『数学セミナー』1993年９月号から抜粋しておく. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 読者は, フェルマー予想が解かれたと発表され, それが確からしいというニュースをご存じであろう. これは, プリンストン大学のワイルス教授が, ケンブリッジ大学のニュートン研究所において６月末に行われたシンポジウムで明らかにしたことだが, その模様について筆を走らせてみることにする. この研究所の今年１月から６月までの２つのテーマのうちの１つが「\(L\,\)関数と数論」であった. そして６月の末に「\(p\,\)進表現, 岩澤理論, モチーフの玉河数」と題するこのテーマを締めくくるシンポジウムが行われ, ワイルスはここで１時間講演を３回行った. ワイルスが解いた (と発表した) のは, 半安定な楕円曲線に対する谷山-志村予想である. 数学の理論の上からは谷山-志村予想の方が単発的な興味の対象であるフェルマー予想より, ずっと価値のあるものである. ワイルスの講演の題目は「保型形式, 楕円曲線, ガロア表現」で, これからは谷山-志村予想もフェルマー予想も察することはできない. 彼の講演は朝の10時から１時間ずつ組まれていたが, １回目と２回目の講演では谷山-志村もフェルマーもまったく口にしなかった. 彼はこの２回の講演で笑みを絶やさず話し続け, メイザーのガロア表現の変形理論に関する見事な結果について述べた. ２回目の講演の後, 明日はこの理論を楕円曲線に応用すると, つぶやくように言って黒板を離れた. 次の日, 僕がセミナールームにはいると, もう部屋はたくさんの人で一杯で, 不思議なことにカメラを持った人たちが４,５人いた. ワイルスが話し始め, 30分が経過してワイルスが黒板に谷山-志村予想 (半安定な曲線に対する) を「定理」として述べたとき, 初めてその意味が分かった. 僕は驚きで目を凝らして黒板を見てしまったので, 周りの人々がどんな反応を示したのか覚えていない. しかし, 大部分の人たちにとっては, 驚きで息が止まるような一瞬であったことも間違いないのである. この日のワイルスの話しぶりは前日までと少しも変わらず淡々として気負うところなどまったくないものだった. そして最後に |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 系 \(x^{\!\:p}\!+y^{\!\:p}\!+z^{\!\:p}\!=0,\:\:\:x,\,y,\,z\,\)が有理数, \(\:p\!>\!2\,\)ならば\(\,xyz\!=\!0\) | ||||||||||||||||||||||||||||||||||||||||||||||||||
| として, フェルマー予想が解決されたことを静かに宣言した. 次の講演者はリベットだった. 彼はワイルスの書いた上の系の部分だけを四角で囲って, 自分の講演の最中にも残し, 消さないようにつとめていた. しかし, 調子に乗りはじめて\(\,x^{\!\:p}\,\)のところを消してしまった. これはしまったと\(\,x^{\!\:p}\,\)を自分で書き直したのだが, これはフェルマー予想の証明の３分の１がリベットの貢献によることを象徴するようなできごとだった. ワイルスの使ったアイディアの中で日本人の貢献も少なくないことを書いておきたい. まず, 谷山豊氏, 志村五郎氏の貢献は言うまでもないが, 肥田晴三氏の理論はここで本質的に使われている. メイザーの変形理論を始めワイルスに基本的アイディアを与えた多くの理論は, 岩澤理論に端を発している. 証明のポイントの１つである, ある種のコホモロジーの位数の計算は, この場合のブロック-加藤 (和也) の玉河数予想を確かめることに他ならない. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ～ 栗原将人『６月23日 ニュートン研究所でのワイルスの講演』～ | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| 1991年の頃であったと思う. 私は, 大学における代数学の講義の中で\(\,\textrm{FLT}\,\)の存在を初めて知った. 単純な問題に見えたが, 予想だけを書き残したフェルマーの死後, 320年以上を経た今でも未解決であるという事実に驚いた. それ以降, 大学の図書館で数論に関する書籍を漁った. 丸善や紀伊國屋や (神保町の) 明倫館へ行って, 入手しうるものを買い求めた. 正直に言えば, 難解で全く歯が立たなかった (歯を折られた) 専門書も数多い. しかし, \(\,\textrm{FLT}\,\)の解決を目指して多くの数学者たちが孤軍奮闘した情熱と, そこから生じた数学史上の数々のドラマを知って感激した. 大学の図書館にあったディリクレ / デデキント『整数論講義』(共立出版) は, 微に入り細に渡って論述するスタイルが採られており, 最初に読むにはやや敷居が高く感じられた. 一方, 高木貞治『初等整数論講義』(共立出版) は, 整数の初歩から二次体までが丁寧に解説されていて読み易い. 私は, まずこれを熟読した. 大学の購買部で見つけたヴェイユ『初学者のための整数論』(現代数学社) やアルティン『ガロア理論入門』(東京図書) も読み易かった. 同じく購買部で見つけた永田雅宜『可換体論』(裳華房) により, 私は (位相や付値を含む) 代数的知識の初歩を習得した. 高木から永田までの４冊は, 現在に至るまで私の愛読書である. 高木貞治『代数的整数論』(岩波書店) は, 当時は品切れ (重版未定) であった. 明倫館で古書を発見したが, 高額で学生には手が出せない. 復刻を要求すべく (大学の購買部を通じて) 岩波書店に繰り返し発注し, 後に入手した. この本は, 前編の代数体の一般論は何とか読めるが, 後編の類体論は読みづらく, 解読が難しいものであった. 群のコホモロジーを用いて類体論を再構成した彌永昌吉『数論』(岩波書店) を書店で入手した. これも俄か勉強の学部生が読める代物ではなく, アデール環やイデール群には辟易させられた. ただし, 附録の「類体論の成立」は大変に面白い. コホモロジーを用いずに類体論の概要を解説した河田敬義『数論』(岩波書店) や, ゼータ関数や保型関数など解析的数論の要点を簡潔にまとめた藤崎源二郎 / 森田康夫 / 山本芳彦『数論への出発』(日本評論社) は, 解説が丁寧で興味深く読める (前者には素数定理の証明もある). この２冊も私の愛読書である. 数論をより深く学びたいと考えた私は, 代数幾何にも興味を抱いた (私の学生時代に京都大学の森重文氏がこの分野でフィールズ賞を受賞したことからの影響もあった). 専門書ではないが, 飯高茂 / 上野健爾 / 浪川幸彦『デカルトの精神と代数幾何』(日本評論社) は極めて面白い. 代数幾何の興味深い話題がアラカルト的に採り上げられており, 私が再三熟読したものである. 彌永昌吉 / 布川正巳『代数学』(岩波書店) や河田敬義『ホモロジー代数』(岩波書店) を併用しつつ, 宮西正宜『代数幾何学』(裳華房) や岩澤健吉『代数函数論』(岩波書店) にも触手を伸ばした. これらは具体例のない抽象的議論を中心とする内容で, 解読は容易ではない. しかし私は, 大学卒業後も再三再読して理解に務めた. 彌永昌吉, 河田敬義, 岩澤健吉などの著名数学者たちへの強い憧憬が, 私の数学に対する熱意を支えてくれたように思う. M.リード『初等代数幾何学講義』(岩波書店) や上野健爾『代数幾何入門』(岩波書店) は, 他の専門書にはない具体例が豊富である. 特に後者の「特異点解消定理」(フィールズ賞を受賞した広中平祐氏の業績) には魅了された. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| 当時の私が興味の赴くままに書籍渉猟を進める中で見つけたのが, 栗原将人氏による前掲の文章である. 数学界は大変な騒ぎであったが, 肝心のワイルズの論文がなかなか発表されない.
査読者による指摘でワイルズの証明の論理にギャップが見つかったことが後に判明した.『数学セミナー』1994年２月号には, 朝日新聞からの引用とともに次のような記事が掲載された. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 解決したかに見えた「フェルマーの最終定理」の証明が, 最後の局面で難航していることがわかった. A.ワイルズ教授が, 再点検の過程で未解決の問題に突き当たったことを打ち明ける声明を発表.
教授の声明は, 数学者向けに状況を説明したもので「ほとんどの問題は解決したが, 一つがまだ解けていない」としている. 一方で「近い将来に完了できると確信している」との自信も見せ,「２月に始まるプリンストンでの講義で, この仕事の全容をお話しできる」としている. (12月９日朝日新聞夕刊より) |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ～『数学セミナー』1994年２月号「掲示板」～ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 実際には, ワイルズがそのギャップを埋めることに成功して解決を再発表したのは, 1994年の後半になってからであった. ここで, 私の手元にある当時の新聞記事から抜粋する. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 350年余も数学の超難問だった「フェルマーの最終定理」の証明に, あと一歩の難関に阻まれていた米プリンストン大のアンドリュー・ワイルズ教授らが,
ついに証明に成功したようだ, との電子メールが世界の数学者を駆け巡り, 注目を集めている. 論文を見ている人はまだ限られているが, 証明の方針は多くの数学者を納得させ,「今度こそ本物か」と,
期待が高まっている. ワイルズ教授は昨年６月, 英国での講演で「証明」を宣言したが, 同12月になって未解決の壁にぶつかった, と声明を出した. その最終局面の難題を, ワイルズ教授らは英国での講演で示したのとは別の方法で解決したという. 今度の証明は, だ円曲線に関するワイルズ教授の論文と, ある集合の性質を論じ, 先の難題を解決したテイラー教授との共同論文の２本からなるという. 東京工業大数学科の加藤和也教授 (整数論) は「証明の方針は, なるほどと思わせるものだ. 近く発表されるだろう論文を早く見たい」と話している. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ～「朝日新聞」1994年10月28日～ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 数学界の難問として有名な「フェルマーの最終定理」を米プリンストン大学のアンドリュー・ワイルズ教授が証明に成功した可能性が27日までに出てきた.
ワイルズ教授は昨年６月にも, ８年間の研究の後で同定理を証明したと発表したが, 専門家から200ページに及ぶ論文の誤りを指摘され,「証明は完全ではなかった」と認めていた.
同教授はその後, かつての教え子で現在はケンブリッジ大学教授のローレンス・テイラー氏と協力して, 昨年の証明法の問題点を解決. プリンストン大に論文を提出するとともに 26日に米国の約20人の数学者に論文を送った. ワイルズ教授の論文を受け取った数学者の一部は, 論文に誤りがないかどうか分かるまでには数週間を要するとしているが, プリンストン大学の同僚の一人は「今回の論文は万全のようだ」と述べている. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ～「毎日新聞」1994年10月28日～ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 翌年 (1995年) になると, \(\,\textrm{FLT}\,\)に関する講演会や公開講座が各地で開催された. 私は, 既に大学を卒業して甲府にある私立の中高一貫校に勤務していたが, これらの講義を聴くため (土日には) 都内に通い続けた. 以下, 手元にある備忘録に基づいて記憶を辿る. 1995年１月, 上智大学において加藤和也氏による講演「類体論について」を興味深く聴いた. 当時, 東京工業大学の教授であった加藤和也氏は, 同じ頃, 大岡山キャンパスにおいて連続講義を始められた. ガロア理論や楕円曲線論から始まり, 代数多様体の特異点解消や分類理論にいたる内容であり, 極めて面白かった. 加藤教授自身については, 高次元類体論のオーソリティーであるにも拘らず, 講義におけるその口調から, 謙虚で温厚な人柄という印象を受けた. 加藤教授ならば, 恐らくワイルズの査読用論文を入手されていることであろう. 講義が終わってから, 私は彼の研究室を訪れた. 論文をコピーしたかった私は,「すぐにお返しするので, 論文をお借りしたいのですが」と申し出た. すると加藤教授は「それではこれを差し上げましょう」と, 近くの棚の上に置いてあった論文 [W] のコピーを即座に手渡してくださった. それは, (ワイルズ自身のものと思われる) 手書きの推敲の跡を含む139枚にも及ぶ厚い冊子 (R.テイラーとの共著論文 [TW] を含む) であった. [W] が "Annals of Mathematics" に発表されたのは1995年の５月のことであるから, 私はそれ以前にこの論文を入手できたわけで, 加藤教授のご厚意には大変感激した. 同年４月からは, 八王子に移転して間もない東京都立大学に通い, 栗原将人氏による「楕円曲線」に関する連続講義を何週かに渡って聴講した. また, 同年７月には, 加藤和也氏による「フェルマーの最終定理」と題する２日間の連続講義 (お茶ノ水女子大学主催) を聴き, 水元信一郎氏による「ゼータ関数と数論」関係の講義 (東京工業大学主催) を聴いた. 10月には, 学習院大学において足立恒雄氏 (早稲田大学) や田口雄一郎氏 (東京工業大学) によるフェルマー予想の歴史やワイルズの証明の概要に関する講義を聴き, 東京工業大学において藤田隆夫氏による代数幾何学の初歩に関する連続講義を聴いた. 11月には津田塾大学において足立恒雄氏による「フライによるフェルマーの最終定理の谷山予想への還元」や上野健爾氏 (京都大学) による「20世紀代数幾何学～重複度と交点数を巡って」などを聴講した. 翌1996年８月には東京女子大学において加藤和也氏による「フェルマーの最終定理を巡って」と題する講義を聴き, 1997年１月の新春特別講義 (京都大学主催) では斎藤秀司氏 (東京大学) による講義「フェルマーからゼータへ」を聴いた. 1998年にも東京大学において堀川頴二氏や斎藤毅氏による楕円曲線に関する興味深い講義や加藤和也氏による\(\,\mathrm{FLT}\,\)関連の講演を聴いた. 加藤教授から頂いた論文 [W] を読んでみた. 冒頭の "Introduction" は興味深く読めたが, 当然ながら本文については全く理解できない. それでも私は丹念に１ページずつ目を通し,「現代数学の最先端に触れている」ことを実感した. この "Introduction" (緒言) については §４.で詳述する. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| §３．解決までの過程 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\textrm{FLT}\,\)を示すためには, \((1.1)\,\)において\(\,n\!=\!4\,\)および\(\,n\!=\!p\,\)(奇素数) の場合を示せば十分である.
\(n\!=\!4\,\)すなわち\(\,x^{\!\:4}\!+\!y^{\!\:4}\!=(z^{\!\:2})^{\!\:2}\,\)の場合については, 原始ピタゴラス数\[(x,\,y,\,z)=(u^2\!-\!v^2,\,2uv,\,u^2\!+v^2),\:\:(u,\,v)=1\tag{3.1}\] を用いた無限降下法によるフェルマー自身の証明が「本の余白」ではない他の場所に残されている. \(n\!=\!p\,\)すなわち\[x^{\!\:p}\!+\!y^{\!\:p}\!=\!z^{\!\:p}\tag{3.2}\]については, まず, \(\,p\!=\!3\,\)の場合について, オイラー (Leonhard Euler, 1707-1783) が細かな場合分けを含む背理法により証明した. その証明は, 立方数の各素因数を立方数であると不用意に断定 (整数環\(\,\mathbb{Z}\,[\sqrt{-3\!\:\!\:}\,]\,\)に素元分解の一意性を根拠を明確にせずに適用) した点で不備があった (実は他の方法で彼が既に正確な証明を得ていたことが後に判明した). 一方, ガウス (Carl Friedrich Gauß, 1777-1855) は, 円分体\(\,\mathbb{Q}\,(\zeta_{\!\:3})\,\)の整数環\(\,\mathbb{Z}\,\!\:[\!\:\zeta_{\!\:3}\!\:]\,\)における素元分解の一意性を用いた無限降下法により, 最初から完全なる証明を得ている. \(p\!=\!5\,\)の場合については, ディリクレ (Peter Gustav Lejeune Dirichlet, 1805-1859) が実二次体\(\,\mathbb{Q}\,(\sqrt{5\!\:\!\:}\!\:)\,\)の整数環を用いて\(\,xyz\equiv0\:\:\textrm{mod}\:10\,\)の場合のみを示し, ルジャンドル (Adrien-Marie Legendre, 1752-1833) が他の場合を補う形で証明した. \(p\!=\!7\,\)の場合については, ラメ (Gabriel Lamé, 1795-1870) が示したが, その方法は複雑を極めた上に不備があった. 後に, ルベーグ (Victor-Amédée Lebesgue, 1791-1875) が簡略化した証明を発表した. \(\textrm{FLT}\,\)の証明は, その初期の段階では個々の\(\,p\,\)に応じた証明法が編み出された. この方法で証明を進める限りでは, (§１. における「反例探し」と同様) \(\textrm{FLT}\,\)の完全解決は永久に見込めない. もう少し効率のよい包括的な証明法を試行錯誤する必要がある. より広範な\(\,p\,\) に対して最初に結果を得たジェルマン (Sophie Germain, 1776-1831) は, \(\,\textrm{FLT}\,\)を\[\begin{cases}\:xyz\not\equiv0\\ \:xyz\equiv0^{{}^{ }}\end{cases}\:\textrm{mod}\:p\]の２つの場合に分け, \(\,p,\:2p\!\!\:+\!1\,\)が共に素数 (\(\,p\,\)がジェルマン素数) ならば, 前者の場合は\(\,\textrm{FLT}\,\)が真であることを証明した. ラメは, \(\,\mathbb{Z}\,[\!\:\zeta_{p}\!\:]\:\left(\zeta_{p}\!=e^{\frac{2\!\:\!\:\pi\!\:\!\:i }{p}}\right)\,\)において\(\,(3.2)\,\)を\[x^{\!\:p}=\prod_{k=0}^{p-1}\,(z\!-\!{\zeta_{p}}^{\!k}y)\]と変形して (オイラーと同様の手法で) \(\textrm{FLT}\,\)を解決しうると発表したが, リューヴィル (Joseph Liouville, 1809-1882) に右辺の分解の一意性に関して疑義を挟まれ, ラメはその解決に失敗している. クンマー (Ernst Eduard Kummer, 1810-1893) は, 多年の苦心の末, 素因数をさらに細かく分解しうる理想数 (後に付値やイデアルへと理論整備される) を考案し, 分解の一意性を確立する方法を考案した. 彼は, \(\,\mathbb{Z}\,[\zeta_{p}]\,\)の単数群やイデアル類群の位数 (類数) \(h_{p}\,\)を綿密に考察し, \(\,p\!\!\not\!\!\:\!\:|\,h_{p}\,\)なる正則素数\(\,p\,\)について\(\,\textrm{FLT}\,\)を証明している. クンマーの研究は, 代数的整数論の礎を築いたのみならず, ベルヌーイ数\(\,B_{n}\,\)を用いた非正則素数の判定法\(\,p\,\Large{|}\normalsize{\,\displaystyle{\prod_{n=1}^{\frac{p\!\:-\!\:3}{2}}B_{2n}}}\,\)により, 整数論とゼータ関数 (解析的整数論) との関連性を示した (後の岩澤理論の萌芽となる) 点で画期的と言えよう. 周知の通り, 当時の数論界には, ガロア (Évariste Galois, 1811-1832) の理論, ガウスの相互法則, ディリクレの二次体論や\(\,L\,\)関数, デデキント (Richard Dedekind, 1831-1916) のイデアル論やクンマーの円分体論を経たクロネッカー（Leopold Kronecker, 1823-1891）のアーベル拡大の理論など, 味わい深い理論が豊富に存在する. \(\textrm{FLT}\,\)の存在がこれらの理論の発展を促したことは特筆されてよいが, これ以後, この方面からは\(\,\textrm{FLT}\,\)解決への進展は停滞していくことになる. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
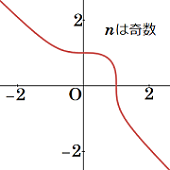
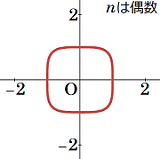
| 原始ピタゴラス数\(\,(3.1)\,\)が単位円\(\,x^2\!+y^2\!=\!1\,\)上の有理点から得られるように, \(\,\textrm{FLT}\,\)は, フェルマー曲線\[F_{n}:x^n\!+y^n\!=\!1\:\:(n\!\geq\!3)\] | ||||||||||||||||||||||||||||||||||||||||||||||||||
  |
||||||||||||||||||||||||||||||||||||||||||||||||||
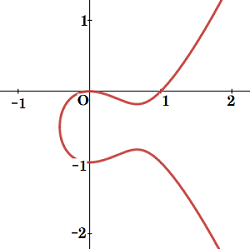
| 上の有理点の存在問題として捉えられる. \(F_{n}\,\)は非特異 (\(F_{n}\,\)上の任意の点で\(\,x,\,y\,\)の偏微分係数が同時に\(\,0\,\)にはならない) 代数曲線で, 且つ, その種数は \(g\!=\!\displaystyle{\frac{(n\!-\!1)(n\!-\!2)}{2}}\) である. \(F_{n}\,\)において\(\,n\!\geq\!4\,\)ならば\(\,g\!\geq\!3\,\)であり, これについて, モーデル (Louis J. Mordell, 1888-1972) が予想し, 後にファルティングス (Gerd Faltings, 1954- ) が証明した定理「種数が\(\,2\,\)以上の\(\,\mathbb{Q}\,\)上で定義された代数曲線は有限個の有理点しかもたない」は, \(\,\textrm{FLT}\,\)に反例が存在するとしても高々有限個であることを主張する. \(\,F_{n}\,\)において\(\,n\!=\!3\,\)ならば\(\,g\!=\!1\,\)であり, 射影平面\(\,\mathbb{P}^2\)上で適当な変数変換を施せば (ワイエルシュトラス標準形に直せば)\(\,F_{n}\,\)は楕円曲線になる. これについて, \(\,\mathbb{Q}\,\)上の楕円曲線 (特定の有理点をもつ種数が\(\,1\,\)の非特異な代数曲線)\(\,E\,\)上の有理点に無限遠点\(\,\textrm{O}\,\)を加えた解集合\(\,E\,(\mathbb{Q})\,\)は, 有限生成アーベル群をなし, \(\,E\,(\mathbb{Q})\simeq\mathbb{Z}^{{\!\:}^{r}}\!\times(\)有限群\()\,\)と表せることをヴェイユ (André Weil, 1906-1998) が示している. 20世紀の中頃になって, アイヒラー (Martin Eichler, 1912-1992) は, 楕円曲線\[E_{1}:y^2\!+y=\!x^3\!-x^2\] |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| の\(\,L\,\)関数\(\,L\,(s,E_{1})\,\)と保型形式\(\,f_{1}\,\) \[f_{1}=q\,\displaystyle{\prod_{n=1}^{\infty}}\,(1\!-q^n)^2(1\!-q^{11n})^2\]の\(\,L\,\)関数\(\,L\,(s,
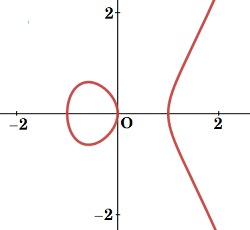
f_{1})\,\)が全ての素数に対して一致することを示した. 以下, 少し解説する. 楕円曲線\(\,E\,\)は, 適当な変数変換を施せば\[y^2\!=x^3\!+\!ax\!+\!b,\:\:\varDelta\!\:(E\!\:)\!\not=0\]の形に変形できる (\(\varDelta\) は判別式). その有理点を探すことは容易ではないが, \(\,a,\,b\in\mathbb{Z}\,\)として, 有限体\(\,\mathbb{F}_{p}\,\)で還元した格子点は比較的容易に見つかる. 例として \[E_{2}:y^2\!=x^3\!-\!x\] |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| をとれば, | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\mathbb{F}_{2}\,\)では\(\,(0,\,0),\,(1,\,0)\,\)の\(\,2\,\)個 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\mathbb{F}_{3}\,\)では\(\,(0,\,0),\,(1,\,0),\,(2,\,0)\,\)の\(\,3\,\)個 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\mathbb{F}_{5}\,\)では\(\,(0,\,0),\,(1,\,0),\,(2,\,1),\,(2,\,4),\,(3,\,2),\,(3,\,3),\,(4,\,0)\,\)の\(\,7\,\)個 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| が解であり, 解の個数を\(\,N_{p}(E_{2})\,\)として\(\,\textcolor{magenta}{a_{p}(E_{2})}\!=p-N_{p}(E_{2})\,\)とおけば, | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| を得る. これに対し, \(\,q\,\)を\(\,\tau\,\)の関数として\[f_{2}(\tau)=q\,\displaystyle{\prod_{n=0}^{\infty}}\,(1\!-\!q^{4n})^2(1\!-\!q^{8n})^2 =\sum_{n=1}^{\infty}\textcolor{magenta}{a_{n}(f_{2})}\!\:q^n\]を考えると, \[f_{2}(\tau)=q\textcolor{magenta}{-\!2\!\:}q^5\!-\!3\!\:q^9 \textcolor{magenta}{\!+\!6}\!\:q^{13}\textcolor{magenta}{\!+\!2}\!\:q^{17}\!-\!q^{25} \textcolor{magenta}{\!-\!10}\!\:q^{29}\textcolor{magenta}{\!-\!2}\!\:q^{37} \textcolor{magenta}{\!+\!10}\!\:q^{41}\!+\cdots\]という興味深い現象が生じる. アイヒラーは \(E_{1}\) に関してこれと同様の発見をしたのである. \(E_{2}\,\)を, 適当な変数変換を施して\(\,|\varDelta\!\:(E_{2})|\,\)を最小にした極小ワイエルシュトラス標準形と捉え直すと, \(\,E_{2}\,\)は\(\,p\!=\!2\,\)で悪い還元をもつ (\(E_{2}:y^2\!=\!x\!\:(x\!+\!1)^2\)であるから\(\,E_{2}\,\)は\(\,\mathbb{F}_{2}\,\)において楕円曲線にならない) が, これは乗法的還元であるから, \(\,E_{2}\,\)は半安定な楕円曲線である. 精密に議論する際は, (既述の通り) 楕円曲線\(\,E\,\)を非特異射影代数曲線として捉え, 無限遠点を加えて\(\,\textcolor{magenta}{a_{p}(E\!\:)}\!=1\!+p-\!N_{p}(E)\,\)とおく. 良い還元をもつ\(\,p\,\)について, ハッセ (Helmut Hasse, 1898-1979) は, \(\,\textcolor{blue}{|}\,\textcolor{magenta}{a_{p}(E\!\:)}\,\textcolor{blue}{|\:<\!2\sqrt{p\,}}\,\)が成り立つことを示している. \(\mathbb{Q}\,\)上の楕円曲線\(\,E\,\)の\(\,L\,\)関数は\(\,E\,\)の導手\(\,N\,\)(良い還元をもたない素数の積) を用いたオイラー積 \[L\,(s,\,E\!\:)=\prod_{p\,\!\not\,|\,N}^{}\left(1-\frac{\textcolor{magenta}{a_{p}(E\!\:)}}{p^s}+\frac{p}{p^{2s}}\right) \cdot\prod_{p\,|\,N}^{}\left(1-\frac{\textcolor{magenta}{a_{p}(E\!\:)}}{p^s}\right)\]であり, これを, ディリクレ級数の形\[\,L\,(s,\,E\!\:)=\displaystyle{\sum_{n=1}^{\infty}}\,\frac{a_{n}(E\!\:)}{n^s}\]で表したものが\(\,E\,\)から定義されるゼータ関数\(\,\zeta_{E}(s)\,\)である. 一方, \(\,f_{2}(\tau)\,\)は, 重み\(\,2\), レヴェル\(\,32\,\)の保型形式 (正規化された同時固有カスプ形式), すなわち\[f\left(\displaystyle{\frac{az\!+\!b\,}{cz\!+\!d\,}}\right)=(cz\!+\!d\,)^2 f\,(z)\:\:\:(a,\,b,\,c,\,d\in\mathbb{Z},\:\:\:ad\!-bc\!=\!1,\:\:\:c\equiv0\:\textrm{mod}\:32\,)\tag{3.3}\]\[f\!\:(\tau)=\displaystyle{\sum_{n=1}^{\infty}}\,{a_{n}(f\,)}\!\:q^n\:\:(q=e^{2\pi i\tau})\tag{3.4}\]をみたす上半平面\(\,\mathfrak{H}\,\)上の正則関数 (且つフーリエ展開される周期関数) であり, \(\,(3.4)\,\)を\[L\,(s,\,f\!\:)=\displaystyle{\sum_{n=1}^{\infty}}\,\frac{a_{n}(f\,)}{n^s}\]と表したものが, \(\,f\,\)から定義されるゼータ関数である. アイヒラーの発見を契機として, ゼータ関数を媒介とした楕円曲線\(\,E\,\)と保型形式\(\,f\,\)の関係が研究されることになる. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| アイヒラーの発見の少し後に,「任意の楕円曲線\(\,E\,\)に対し, \(\,q\,\)展開の\(\,q^{p}\,\)の係数に\(\,a_{p}(E\!\:)\,\)をもつ保型形式\(\,\displaystyle{\sum_{n=1}^{\infty}}\,a_{n}(E\!\:)\,q^n\,\)が対応する」という, 谷山・志村予想が知られるようになる. これは, \(\,E_{2}\,\)に対して全ての素数\(\,p\,\)について\(\,\textcolor{magenta}{a_{p}(E_{2})\!=\!a_{p}(f_{2})}\,\)をみたす保型形式\(\,f_{2}\,\)が対応したのと同様, 任意の半安定な楕円曲線に対して必ず或る保型形式が対応することを意味する. 谷山豊 (Yutaka Taniyama, 1927-1958) が提示し, 志村五郎 (Goro Shimura, 1930- ) が定式化したこの予想は, 換言すれば,「\(N\,\)を導手とする\(\,\mathbb{Q}\,\)上の楕円曲線\(\,E\,\)には, モジュラー曲線\(\,X_{0}(N)\,\)から射影代数曲線\(\,E\,\)への\(\,\mathbb{Q}\,\)上の有理写像\(\,X_{0}(N)\to E\,\)が必ず存在する」となる. \((3.3)\,\)で与えられるモジュラー関数 (リー群\(\,G\,\)上の関数で\(\,G\,\)の離散的部分群\(\,\varGamma\,\)で不変な保型関数のうち\(\,G\!=\!\textrm{SL}\!\:(2,\,\mathbb{R}),\,\varGamma\!=\!\textrm{SL}\!\:(2,\,\mathbb{Z})\,\)であるもの) を例にとれば, 合同部分群\(\,\varGamma_{0}(32)\,\)の (\(\mathfrak{H}\,\)に無限遠点を付加した) \(\mathfrak{H}^{*}\,\)による非特異射影代数曲線\(\,X_{0}(32)\backslash\mathfrak{H}^{*}\,\)がモジュラー曲線\(\,X_{0}(32)\,\)である. 「\(\mathfrak{H}\,\)上の, 重み\(\,2\), レヴェル\(\,1\,\)または\(\,2\,\)の保型形式は\(\,0\,\)に限る」から, 谷山・志村予想は, このような保型形式から得られる曲線はモジュラーな楕円曲線ではないことを主張する. ここで, フライ (Gerhard Frey, 1944- ) は, \(\,\textrm{FLT}\,\)の反例, すなわち\[a^{\!\:p}\!+b^{\!\:p}\!=\!c^{\!\:p},\:\:a\!\equiv\!3\:\textrm{mod}\:4, \:\:b\equiv\!0\:\textrm{mod}\:2,\:\:p\!\geq\!5\]をみたす\(\,a,\,b,\,c\,\)を用いて, \(\,p\,|\,abc\,\)なる素数\(\,p\,\)で乗法的還元をもつ半安定な楕円曲線\[E_{3}:y^2\!=x\,(x\!-\!\!\:a^{\!\:p})(x\!+\!\!\:b^{\!\:p})\]を構成した. 一般に, 楕円曲線\(\,E\,\)の\(\,p\,\)分点全体への絶対ガロア群\(\,\textrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\,\)の作用\(\,\rho\,\)によるガロア表現\[\rho:\textrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\to\textrm{GL}_{2}(\mathbb{F}_{p})\,\]は (閉部分表現をもたない) 絶対既約である. セール (Jean-Pierre Serre, 1926- ) は,「このような表現の中で複素共役の像の行列式が\(\,-1\,\)のものは全て保型形式を構成できる」と予想した. さらに, リベット (Ken Ribet, 1948- ) は,「半安定な楕円曲線から得られる表現が保型形式をもつならば, セール予想が指示する通りの重さやレヴェルをもつ保型形式が得られる」というセール予想の一部 (\(\epsilon\,\)予想) を証明した. 具体的には, これを\(\,E_{3}\,\)に適用して, 判別式\(\,\varDelta\!\:(E_{3})\,\)が\(\,(abc)^{2\!\:p}\,\)なる因子をもつことを理由に, \(E_{3}\,\)から得られる保型形式は「重み\(\,2\,\), レヴェルが\(\,2\,\)」であること, すなわち\(\,E_{3}\,\)が, 谷山・志村予想に反する「モジュラーではない楕円曲線」であることを指摘する. これにより, \(\,\textrm{FLT}\,\)は, 半安定な楕円曲線についての谷山・志村予想の解決に帰着され, ワイルズがこれを証明したことで, \(\,\textrm{FLT}\,\)はようやく解決されたのである. ワイルズはどのようにして谷山・志村予想の証明に至ったのか. その概略について, ワイルズの論文を引用しつつ, 次節で見ていくことにする. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| §４．Wilesによる解説 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| (先述したように) 私が加藤和也教授から直接に頂いたワイルズの論文 [W] は, これが Annals of Mathematics に掲載される前の,
校正用原稿のコピーであった. 本論は私の理解しかねる内容であったが, \(\textrm{FLT}\,\)解決への過程や証明の方針, ワイルズ自身の苦心談を報告した「緒言 (Introduction)」は大変に興味深い.
以下, [W] から少し抜粋する. なお, Annals of Mathematics に掲載された [W] には後に追記された部分が含まれるため, そのページ数は (私の手元にあるコピー原稿より) 若干増加している. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| \(\mathbb{Q}\,\)上の楕円曲線は, \(\,X_{0}(N)\,\)のモジュラー曲線で有限被覆ならばモジュラーである. 志村と谷山による予想は\(\,\mathbb{Q}\,\)上の全ての楕円曲線はモジュラーであると主張する. この予想はヴェイユ (Weil) の1967年の論文が出版されてようやく広く知られるようになった. 1985年, フライ (Frey) は, この予想がフェルマー最終定理を意味することに着目した. 両者の厳密な関連のメカニズムについては, セール (Serre) が\(\,\epsilon\,\)-予想として定式化したが, 1986年夏リベット (Ribet) がそれを証明した. リベットの結果は, フェルマーの最終定理の証明を導くには, 半安定な楕円曲線に対して予想が証明されればよいというものであった. 我々は, ガロア表現と結び付けて楕円曲線を研究する. \(\,\rho_{p}\,\)は\(\,\mathbb{Q}\,\)上の楕円曲線の\(\,p\,\)分点における\(\,\textrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\,\)の表現であるとする. \(\,\rho_{3}\,\)が既約ならばそれはモジュラーであるというラングランズ (Langlands) とタンネル (Tunnell) の決定的な重要な定理のために\(\,3\,\)の選択は決定的である. 我々は, 他の素数での\(\,\rho\,\)の分岐に対してある柔軟な制限を行って, \(\,\rho_{3}\,\)が\(\,3\,\)で半安定であるという仮定の下で\(\,\rho_{3}\,\)の全ての適切な持ち上げはモジュラーであることを示す必要がある. 論文 [TW] を援用して我々はこの問題を解決した. このことは, 同伴\(\,3\,\)進表現がモジュラーのとき, そのときに限り\(\,E\,\)はモジュラーであるという, \(\,E\,\)のモジュラリティーを証明するには十分である. 議論の展開の鍵は, 数論における異なる２つの強い流儀の間の新しく驚異的な結びつきである. 一方に, ガロア表現とモジュラー形式, 他方に\(\,L\,\)関数の特殊値の解釈, である. 前者はより最近のものであり, 1950年代および1960年代のアイヒラー (Eichler) と志村のオリジナルな結果に続いて, 1980年までの間に, ドリーニュ (Deligne), セール, ラングランズによって他の主要定理が証明された. 1980年代半ばから, その分野の主な推進の動機は, \(\,\epsilon\,\)-予想を以前にもまして精巧に仕上げようというセールの諸予想によって与えられた. この問題に関するリベットや他の研究者の研究の他に, 1980年代のさらに特別な発展のいくつか (肥田やメイザー (Mazur) の研究) を用いなければならない. ２番目の流儀 (\(L\,\)関数の特殊値に関する流儀) は, ディリクレの有名な解析的関数の定理にまで遡るが, その現代版であるバーチおよびスウィナートン=ダイヤー (Birch and Swinnerton-Dyer) の予想によるものである. 実際には, 我々の分野においては, 岩澤のアイディアによるものであって, かなりの程度まで我々はそれを改変した. ガロア・コホモロジーの原理, 特にポワトゥ (Poitou) とテイト (Tate) の定理はここで重要な役割を果たす. \(\rho\,\)が\(\,3\,\)で既約であるという制限は, \(\,\rho\,\)と共役をもつ楕円曲線族の興味深い議論によって回避できる. このことを使って, 我々は, 全ての半安定な楕円曲線はモジュラーであることを証明した. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ワイルズは冒頭でこのように述べた後, 指標\(\,\chi\,\)の\(\,\textrm{SL}_{2}(\mathbb{Z})\,\)の合同部分群\(\,\varGamma_{1}(N)\,\)に関する重み\(\,k\!\geq\!2\,\)の保型形式\(\,f\,\)と\(\,n\!\in\!\mathbb{Z}\,\)に関するヘッケ作用素\(\,T_{n}\,\)を用いて, 各\(\,n\,\)に対して\(\,T_{n}f\!=\!c\,(n,\,f\,)f\,\)をみたす代数的整数\(\,c\,(n,\,f\,)\,\)と\(\,\chi\,\)をもって\(\,\mathbb{Q}\,\)上で生成された数体\(\,K_{f}\,\)と, その整数環\(\,\mathcal{O}_{f}\,\)を定義する. \(\,\mathcal{O}\,\)の任意の素数\(\,\lambda\,\)での完備化\(\,\mathcal{O}_{f,\,\lambda}\)に対して, 次の 定理\(\,01\,\)を掲げる. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 定理\(\,01\) \(\mathcal{O_{f}}\,\)の各素数\(\,\lambda\!\:|\!\:p\,\)に対し, \(Np\,\)を割る素数を除外すれば不分岐な連続表現\[\rho_{{}_{\!\!\:f,\,\lambda}}:\mathrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\to
\textrm{GL}_{2}(\mathcal{O}_{f,\,\lambda})\]が存在し, \(q\!\!\not\!\!\:\!\:|\,Np\,\)
なる全ての素数\(\,q\,\)に対して, 次が成り立つ.\[\textrm{trace}\,\rho_{{}_{\!\!\:f,\,\lambda}} (\!\:\textrm{Frob}\,q\!\:)=c\,(q,\,f\,),\:\:\:\textrm{det}\,\rho_{{}_{\!\!\:f,\,\lambda}}(\!\:\textrm{Frob}\,q\!\:) =\chi\,(q)\,q^{k-1}\] |
||||||||||||||||||||||||||||||||||||||||||||||||||
| この後, ワイルズは, 標数\(\,p\,\)の代数的閉包に値をもつ連続表現\(\,\rho_{{}_{0}}\,\)\[\,\rho_{{}_{0}}:\textrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\to \textrm{GL}_{2}(\mathbb{\overline{F}}_{p})\]を提示して, \(\,f\,\)と\(\,\lambda\,\)に対して\(\,\rho_{{}_{0}}\,\)と\(\,\rho_{{}_{\!\!\:f,\,\lambda}}\,\)は\(\,\lambda\,\)を法として\(\,\mathbb{\overline{F}}_{p}\,\)上同型であり, \(\,\mathbb{\overline{F}}_{p}\,\)における\(\,\mathcal{O_{f}/\lambda}\,\)の或る埋め込みであるとき,\(\,\rho_{{}_{0}}\,\)はモジュラーであると明記する. \(\,\mathcal{O}\,\)が局所体（\(\mathbb{Q}_{p}\,\)を含む）の整数環ならば, \(\,\mathbb{\overline{F}}_{p}\,\)における\(\,\mathcal{O}\,\)の特殊な埋め込みに対して, \(\overline{\rho}=\rho\:\textrm{mod}\:\lambda\,\)と\(\,\rho_{{}_{0}}\,\)が\(\,\mathbb{\overline{F}}_{p}\,\)上同型のとき,\[\rho:\mathrm{Gal}\,(\mathbb{\overline{Q}}/\mathbb{Q})\to \textrm{GL}_{2}(\mathcal{O})\]を\(\,\rho_{{}_{0}}\,\)の持ち上げとする. ワイルズは, \(\,\rho_{{}_{0}}\,\)が通常表現か平坦かに場合分けして\(\,\rho\,\)が或るモジュラー形式から生ずるというセール予想の拡張を示す. それを示したのが次の 定理\(\,02\,\)である. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 定理\(\,02\) \(\rho_{{}_{0}}\,\)を既約として, 上の場合分けにおける条件をみたし, モジュラーであるとする. \((1)\) \(\rho_{{}_{0}}\,\)は, \(\mathbb{Q}\left(\!\sqrt{(-1)^{\frac{p\!\:\!\:-\!\:1}{2^{\!\! }}}p\,}\,\right)\,\)へ制限するとき, 絶対既約である. \((2)\) \(q\!\equiv\!-1\:\textrm{mod}\:p\,\)が\(\,\rho_{{}_{0}}\,\)において分岐すれば, \(\,\rho_{{}_{0}}|{}_{D_{q}}\,\)（\(\,D_{q}\,\)は\(\,q\,\)での分解群）が代数的閉包上で可約であるか, あるいは, \(\,\rho_{{}_{0}}|{}_{I_{q}}\,\)(\(I_{q}\,\)は\(\,q\,\)での慣性群) が絶対既約であるか, のいずれかである. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ワイルズは,「最も興味あるケース」として, \(\,p\!=\!3\,\)で, \(\,\rho_{{}_{0}}\,\)が\(\,\mathbb{F}_{3}\,\)で定義できる場合を挙げ, 次の 定理\(\,03\,\)を掲げる. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 定理\(\,03\) \(E\,\)を\(\,\mathbb{Q}\,\)で定義された楕円曲線とし, \(\rho_{{}_{0}}\,\)は\(\,3\,\)分点へのガロア作用とする.
\((1)\) \(E\,\)は, \(\,3\,\)で良い還元または乗法的還元をもつ. \((2)\) \(\rho_{{}_{0}}\,\)は\(\,\mathbb{Q}\,(\sqrt{-3\,})\,\)へ制限するとき, 絶対既約である. \((3)\) 任意の\(\,q\!\equiv\!-1\:\textrm{mod}\:3\,\)に対して, \(\,\rho_{{}_{0}}|{}_{D_{q}}\,\)が代数的閉包上で可約であるか, \(\,\rho_{{}_{0}}|{}_{I_{q}}\,\)が絶対既約であるか, のいずれかである. \(E\,\)が上の３条件をみたすとき, \(E\,\)はモジュラーである. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ワイルズによれば, (平方数の導手をもたない) 半安定の曲線の類は (上の条件の) \((2)\,\)をみたすとは限らないが, \((1)\,\)と\(\,(3)\,\)をみたすという. また, \(5\,\)分点上の表現が, 定理\(\,03\,\)でモジュラーであることが証明された別の楕円曲線に対しても生ずることを示すことで, 定理\(\,02\,\)をこの場合にも適用しうるという (この場合は定理\(\,02\,\)は\(\,p\!=\!5\,\)で適用される). この後, ワイルズは次の 定理\(\,04\,\)を掲げる. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 定理\(\,04\) \(E\,\)を\(\,\mathbb{Q}\,\)上で定義された半安定な楕円曲線とすれば, \(E\,\)はモジュラーである. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| ワイルズはここで, フライによる仮説的な楕円曲線 (§３. における\(\,E_{3}\,\)) がモジュラーではないと指摘したこと, セールが, \(E_{3}\,\)上の\(\,p\,\)分点上の表現は, \(E_{3}\,\)がモジュラーであれば導手\(\,2\,\)のモジュラー形式に結びつくというという予想を提示したこと, 1986年にリベットがこれを証明したことに触れる. そして,「遂に！」という形容詞をもって 定理\(\,05\,\)を掲げた. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 定理\(\,05\) \(u,\,v,\,w\in\!\mathbb{Q}\,\)および\(\,p\!\geq\!3\,\)のとき, \(u^p\!+\!v^p\!+\!w^p\!=\!0\,\)とすれば, \(\,uvw\!=\!0\,\)である. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 最後に, 或る楕円曲線族がモジュラーであることの証明に用いられる 定理\(\,06\,\)(省略) が提示され, 以上が, この論文 [W] の要約として述べられている. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| 論文 [W] における「緒言」の後半は, この定理の証明に至る過程が詳述される. 引き続き, 論文 [W] から抜粋する. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 1986年の夏の終わり, 直接にはリベットの結果を習得するためにこれらの問題の研究を始めた. 数年の間, 総実体に対する岩澤予想の研究とその幾つかの応用に従事していた. その過程で, それらを用いてヒルベルト・モジュラー形式と結びついた\(\,p\,\)進表現に関する結果を発展させた. \(2\,\)進表現での研究を数ヶ月続けた後, 代わりに\(\,3\,\)進表現が使えるのではないかという, この問題の解決のための最初の実質的な突破口が開けた. このことが, 各\(\,n\,\)に対して\(GL_{2}\,(\mathbb{Z}/3^n\mathbb{Z})\,\)表現はモジュラーであるという証明の試みに私を導いた. この時点では, 通常ケースのみを考えていた. この場合の研究から, \(i\!=\!1,\,2\,\)に対する\(\,H^i\,(\textrm{Gal}\,(F_{\infty}/\mathbb{Q}),\,W_{\!f})\,\)の研究に移った. この問題に岩澤理論の適用を試みた. 総実体に対する岩澤予想の証明の中で, 自明な零点を扱うための新たな技巧を導入したが, それは, 円分\(\,\mathbb{Z}_{p}\,\)拡大体を考える標準の岩澤理論を無限に多くの異なる素数\(\,q_{i}\!\equiv\!1\:\textrm{mod}\:p^{n_{i}}\:(\,i\!\to\!\infty\,\)のとき\(\,n_{i}\!\to\!\infty)\,\)の選択に基づく同様の解析に置き換えることを含む. 分岐するコホモロジー群の或る部分群は消滅する, 形式\(\,f\,\)は\(\,\mathfrak{m}\) (\(\,3\,\)を法とする楕円曲線の表現\(\,\rho_{3}\,\)に同伴するヘッケ環の最大イデアル) に対してミニマル・レヴェルで選ばれる, という２つの仮定のもとで, 不分岐なコホモロジー群の良い評価ができたことが収穫であった. 1980年代の後半, 私は, これらのアイディアを環論の言葉に翻訳した. 数年前, 肥田は幾つかのガロア表現の明示的な１パラメータ族を構成していた. この研究を理解するための研究過程でメイザーはガロア表現の変形理論を開発した. メイザーは, 彼が発見した普遍変形環は (少なくとも或る特別な場合には) ヘッケ環であることを解明した. この重要な予想は, モジュラー表現の全ての通常の持ち上げはモジュラーであるという期待を強めた. この環論への翻訳の過程で, 必要とされた\(\,H^2\,\)の部分群に関する消滅の仮定をそのヘッケ環が完全交叉でなければならないという, より強い条件に置き換えなければならないことが分かった. 1991年春, この問題と, その全証明のためのターニング・ポイントが訪れた. ヘッケ環のゴレンシュタイン (Gorenstein) 特性は, 素数レヴェルの場合にメイザーが証明していた. クンツ (Kunz) の論文は, ゴレンシュタイン環の間の同型を調べるために\(\,\eta\,\)不変量を使うことを示唆していた. これとは別に, 私は既に\(\,\mathfrak{p}/\mathfrak{p}^2\,\)不変量が完全交叉の間の同型を調べるのに使えることを確認していた. 完全交叉に対するグロタンディーク (Grothendieck) 双対理論についてのテイトの説明から, この２つの不変量は (そのような環に対して) 等しいことを知った. ゴレンシュタイン環が完全交叉であるための実際的基準であることを理解した. 主要問題にとって, この結果は大変な衝撃であった. (結果として, 主要問題を) 周知のタイプの岩澤理論の類数問題に移せたが, 従来的な方法は, このケースでは全く不十分に思われた. 岩澤理論で使われる体の変換の代わりに, 補助素数を使うアイディアを更に発展させた. ところが, これを使う設定のもとでは, 密接に関係する肥田の構成以外は助けになるとは思えない. 私は, 決定的なものを把握できないまま研究を続けた. 1991年８月, フラック (Flach) の新しい構成法を調べて, セルマー群のサイズの上限を与えるアプローチは, オイラーシステムの構築へ向けての第一歩となるものに思われた. 1992年秋までには, 私はそれを達成しえたと確信して, \(3\,\)を法とする表現が可約である場合について考え始めた. 1993年５月, メイザーの論文のモジュラー曲線の双対形式の構成を読んでいたとき, 突如として驚くべき打開点が現れた. \(\rho_{5}\,\)と共通の楕円曲線族を用いる理論を発見したのである. 今や証明は完成したものと確信し, ケンブリッジで６月21-23日に行われた３つの講演で全理論のスケッチを述べた. しかし, 1993年秋, フラックの方法を拡張するために使ったオイラーシステムの構成は不完全であり, 不備があるかも知れないことが明らかになった. 1994年１月には, オイラーシステムを使う議論の修復のためにテイラー (R.Taylor) が加わった. 1994年春, オイラーシステムの修復が思わしくなかったので, テイラーと共に, \(\,p\!=\!2\,\)を用いる新たな議論を練り始めた. ９月には障害部分を厳密に定式化して, フラックの一般化の議論に一旦区切りをつけることにした. その作業の最中に, 突然の啓示が舞い降りた. 1994年９月19日, 一般化したデ・シャリット (de Shalit) の理論を, 双対性と共に補助的レヴェルでヘッケ環を冪級数環へと接続させれば上手くいくと見通しがついたのである. 私は, 一度捨てた元のアプローチに対してどうしても得られなかった鍵を発見できた. それは, 持ち上げの手続きを達成するために用いた\(\,q_{i}\!\equiv\!1\:\textrm{mod}\:p^{n_{i}}\:(\,i\!\to\!\infty\,\)のとき\(\,n_{i}\!\to\!\infty)\,\)として\(\,q_{i}\,\)を取り出すという, 以前に適用した考えである. この議論をテイラーと話し合った後, 詳細の検討を数日間おこなった. 完全交叉特性を伴う全ての議論は [TW] にある. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 以下, この「緒言」部分の要約が結論としてまとめられ, 今後の課題や関係各位の謝辞が付されて本論へ入ることになる. 数学者がその論文において (背景や過程を含めることはあるが) 苦心談を含めることは極めて珍しい. \(\textrm{FLT}\,\)の解決が, 世界各国の数多くの数学者達の長年に渡る苦心の賜物であったことに鑑みれば, その最後の頂点を極めたワイルズには, その集大成としての苦心談も許されることであろう. ワイルズのように, 解決を宣言した後でその理論の不備を指摘されたときの衝撃や絶望感は, 我々のような素人の想像を絶すると思われる. 解決できなければ, (従来のアマチュア数学愛好家と同様) 結局は単なる人騒がせな売名行為と捉えられかねない. 当然, 数学者としての信用は完全に失墜する. 文字通り致命傷を負うことになり, 自殺に追い込まれかねない事態となる. テイラーの協力でほどなく解決できたワイルズは, その数学的能力や超人的な忍耐力もさることながら, 強力な幸運の持ち主でもあった. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
| §５. 未解決問題の例 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 先述した通り, \(\textrm{FLT}\,\)には定理としての応用価値はない. その価値は, 解決までの過程で夥しい量の新たな数学を産出したことに見出される. 数論には, これと同種の価値をもつ問題が多数存在し, その多くは21世紀を迎えた現在でも未解決である. 実数は (その連続性ゆえに) 解析的な処理が可能であるのに対し, 整数 (素数) は (その離散性ゆえに) 扱いが困難であり, 他の数学の分野に比して未解決問題が多い. 以下, 幾つかの有名な未解決問題を挙げて本稿を終えることにしたい. メルセンヌ (Marin Mersenne, 1588-1648) が構成した\(\,M_{n}\!=\!2^n\!-\!1\,\)なる形の数が素数 (メルセンヌ素数) ならば\(\,n\,\)も素数であるが, 素数\(\,p^{\prime}\,\)に対して\(\,M_{p^{\prime}}\!=\!2^{p^{\prime}}\!-\!1\,\)が素数であるとは限らない. 実際に知られているメルセンヌ素数は (21世紀初頭の時点で) 僅か\(\,20\,\)個あまりであり, これが無数に存在するか否かは未解決である. \(\,M_{p}\,\)がメルセンヌ素数のとき, 偶数の完全数が\(\,2^{p-1}M_{p}\,\)なる形の数に限ることをオイラーが示している. 一方, 奇数の完全数が存在するか否かは未解決である. §3.に登場したジェルマン素数 (\(2p\!+\!1\,\)が素数になる素数\(\,p\,\)) は\(\,\textrm{FLT}\,\)をみたす例を多数与えるが, これが無数に存在するか否かは未解決である. この場合の\(\,2p\!\!\:+\!1\) (安全素数) はメルセンヌ素数\(\,M_{p}\,\)の約数になる. 素数の分布にいかなる規則性が存在するかは, 数論における古くからの難問であった. フェルマーは, \(\,0\!\leq\!n\!\leq\!4\,\)に関して\(\,F_{n}\!=\!2^{2^n}\!-\!1\:(\,n\!\in\!\mathbb{N}\cup\!\{0\})\,\)が素数になることを見出し, \(\,F_{n}\,\)は全て素数であると予想した. しかし, 後にオイラーが\(\,F_{5}\!=\!641×6700417\,\)なる反例を発見している. 以後, \(\,n\!\geq\!5\,\)に関して素数となる\(\,F_{n}\,\)(フェルマー素数) は発見されておらず, 最初の\(\,5\,\)個以外にフェルマー素数が存在するか否かは未解決である. \(\,F_{i}\,\)がフェルマー素数のとき, \(\,m\!=\displaystyle{\!\prod_{i\,\in\,\mathbb{N}}}\:2^kF_{i}\:(\!\:k\!\in\!\mathbb{N}\cup\!\{0\})\,\)ならば正\(\,m\,\)角形は定規とコンパスのみで作図可能であることを, (ガロア理論が広く知られる以前に) ガウスが示している. 「素数が無数に存在する」ことはユークリッド (Euclid, B.C.３世紀頃) 以来よく知られているし, \(\,x\,(\in\!\mathbb{R}^{+})\,\)以下の素数の個数\(\,\pi\,(x)\,\)に関する素数定理\[\lim_{x\to\infty}\frac{\pi\,(x)}{\displaystyle{\frac{x}{\:\log x}\:}}=1\]もド・ラ・ヴァレ・プサン (Charles-Jean de La Vallée Poussin, 1866-1962) やアダマール (Jacques Hadamard, 1865-1963) 以来よく知られている. これらの定理には何通りもの証明法が存在する. 素数を与える多項式の例として, 素数\(\,p\,\)を定数項とする二次式\(\,f_{p}(n)\!=\!n^2\!-\!n\!+\!p\,\)がある. オイラーは, \(\,p\!=\!41\,\)のとき, \(0\!\leq\!n\!\leq\!39\,\)なる全ての\(\,n\!\in\!\mathbb{Z}\,\)に対して\(\,f_{p}(n)\,\)が素数になることを発見した. これに関して, 虚二次体\(\,\mathbb{Q}\,(\sqrt{1\!-\!4p\,})\,\)の類数を\(\,1\,\)とする\(\,p\,\)について, \(\,0\!\leq\!n\!\leq\!p\!-\!2\,\)なる全ての\(\,n\!\in\!\mathbb{Z}\,\)に対して\(\,f_{p}(n)\,\)が素数になることを, フロベニウス (Ferdinand Georg Frobenius, 1849-1917) が示している. 実際には, 類数を\(\,1\,\)とする虚二次体を与える整数はごく僅かしか存在せず, \(\,p\!=\!41\,\)はその最大値になっている (オイラーの鋭い洞察力！). \(\,2\,\)以上の任意の自然数に対して\(\,n\!<\!p\!<\!2n\,\)なる素数\(\,p\,\)が存在することは, ベルトラン (Joseph Bertrand, 1822-1900) が予想し, チェビシェフ (Pafnuty Chebyshev, 1821-1894) がガンマ関数を用いて証明した. 一方, \(\,n^2\,\)と\(\,(n\!+\!1)^2\,\)の間に必ず素数が存在するというルジャンドルの予想は, その簡単な見かけに反して今現在に至るまで証明されていない. また, 双子素数 \((\)素数の組\(\,(p,\,p\!+\!2))\,\)が無数に存在するか否かも有名な未解決問題である. ハーディー (Godfrey Harold Hardy, 1877-1947) とリトルウッド (John Edensor Littlewood, 1885-1977) は, \(\,x\!\in\!\mathbb{R}\,\)以下の双子素数\(\,p\,\)の個数\(\,\pi_{{}_{\!\!\:2}}(x)\,\)を\[\pi_{{}_{\!\!\:2}}(x)\sim\prod_{p}^{}\left(1-\frac{1}{(p\!-\!1)^2}\right)\cdot \prod_{p}^{}\frac{p\!-\!1}{p\!-\!2}\cdot\frac{x}{\log^{\,2\!}x}\]であると予想している (\(\,p\,\)は全ての奇素数を動く). 他にも未解決問題は数多く存在し, 枚挙に暇がない. 以下, \(\,\textrm{FLT}\,\)に関連のある問題のみを挙げておく. ラマヌジャン (Srinivasa Ramanujan, 1887-1920) は, 重み\(\,12\,\)の保型形式 (ヘッケ作用素の同時固有カスプ形式) \[\sum_{n=1}^{\infty}\tau\!\:(n)\,q^n=q\prod_{n=1}^{\infty}\,(1\!-\!q^n)^{24}\:\:(\,q=e^{2\pi i\tau})\,\]で定義されるタウ関数\(\,\tau\!\:(n)\,\)について, その\(\,L\,\)函数\[L\,(s,\,\tau)=\prod_{p}^{}\frac{1}{1-\tau\!\:(p)\,p^{-s}+p^{\,11-2s}}\]における分母の二次式は虚根をもつ (すなわち \(|\,\tau\!\:(p)\,|\leq2\!\:p^{\frac{11}{\!\:2^{\!\! }}}\,\)が成り立つ) と予想した. これは後に一般化され, ドリーニュにより解決された. §３. において, 有限体\(\,\mathbb{F}_{p}\,\)で還元した楕円曲線\(\,E\,\)上の格子点に関わるハッセによる不等式\(\,|\,\textcolor{magenta}{a_{p}(E)}\,|<2\sqrt{p\,}\,\)を挙げた. これを\[\frac{\textcolor{magenta}{a_{p}(E)}}{2\sqrt{p\,}}=\cos\theta_{p}\:\:(\,0\!\leq\!\theta_{p}\!\leq\!\pi\,)\]とおいて, 虚数乗法をもたない楕円曲線について, \(\,p\!\leq\!N\,\)なる\(\,p\,\)の個数\(\,\varphi_{{\!}_{N}}\,\)と, \(\,\alpha\!\leq\!\theta_{p}\!\leq\!\beta\:(\,0\!\leq\!\alpha\!<\!\beta\!\leq\!\pi\,)\,\)をみたす\(\,p\!\leq\!N\,\)なる\(\,p\,\)の個数\(\,\psi_{{\!}_{N}}\,\)について, \[\lim_{N\to\infty}\frac{\psi_{{\!}_{N}}}{\varphi_{{\!}_{N}}} =\frac{2}{\pi}\!\int_{\alpha}^{\beta}\!\sin^{\!\:2}\!\theta\,d\theta\]が成り立つと予想したのが佐藤幹夫 (Mikio Sato, 1928- ) である (2003年現在, 未解決問題). 全ての楕円曲線とモジュラー形式を\(\,L\,\)関数を媒体として関連づける「谷山・志村予想」は, 最近 (1999年) になって, テイラー (Richard Lawrence Taylor, 1962- ) やコンラッド (Brian Conrad, 1970- ) たちによって完全に証明されたようである ([CDT] 参照). これは, ガロア表現と保型表現を\(\,L\,\)関数を媒体として関連づけるラングランズ (Robert Langlands, 1936- ) 予想に含まれる. この予想は多くの問題を含む壮大な構想に基づいており, 2003年現在, やはり解決されていない. |
||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 【文献】 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| [Ｗ] | Wiles, A. "Modular Elliptic-Curves and Fermat's Last Theorem." Ann. Math. 141, pp.443-551, 1995. | |||||||||||||||||||||||||||||||||||||||||||||||||
| [TW] | Taylor, R. and Wiles, A. "Ring-Theoretic Properties of Certain Hecke Algebras." Ann. Math. 141, pp.553-572, 1995. | |||||||||||||||||||||||||||||||||||||||||||||||||
| [R] | Ribet, K.A. "Galois Representations and Modular Forms" Amer. Math. Soc. 32, pp.375-402, 1995 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [Ｆ] | Faltings, G. "The Proof of Fermat’s Last Theorem by R.Taylor and A.Wiles" Notices of Amer. Math. Soc. 42,pp.743-746, 1995 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [CDT] | Conrad, B., Diamond, F., Taylor, R. "Modularity of Certain Potentially Barsotti-Tate Galois Representations" Amer. Math. Soc. 12, pp.521-567, 1999 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [１] | 藤崎源二郎 / 森田康夫 / 山本芳彦『数論への出発 (数学セミナー別冊)』日本評論社, 1980 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [２] | Ribenboim, P. / 吾郷博顕訳『フェルマーの最終定理 13講』共立出版, 1983 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [３] | 彌永昌吉 / 佐々木力『現代数学対話』朝倉書店, 1986 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [４] | 平松豊一 / 宇津木博『フェルマ予想入門』槙書店, 1988 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [５] | Guy, R.K. / 一松信監訳『数論における未解決問題』シュプリンガー・フェアラーク東京, 1990 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [６] | 数学セミナー編集部『数学の最前線』日本評論社, 1990 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [７] | 河田敬義『数論』岩波書店, 1992 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [８] | 『数学セミナー 1993年９月号』pp.20-21, 日本評論社 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [９] | 『谷山豊全集［増補版］』日本評論社, 1994 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [10] | 加藤和也『解決！フェルマーの最終定理 現代数論の軌跡』日本評論社, 1995 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [11] | 栗原将人『Fermat 予想に関する Wiles の仕事の概説』「数学」第47巻４号, pp.394-403, 岩波書店, 1995 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [12] | 足立恒雄『フェルマーの最終定理 第３版』日本評論社, 1996 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [13] | 加藤和也 / 黒川信重 / 斎藤毅『数論３(岩波講座 現代数学の基礎)』岩波書店, 1998 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [14] | 笠原乾吉 / 杉浦光夫『20世紀の数学』日本評論社, 1998 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [15] | 『数学のたのしみ 岩澤数学の全貌 : その豊穣の世界』1999年10月号, 日本評論社 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [16] | Ribenboim, P. "Fermat’s Last Theorem for Amateurs" Springer, 1999 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [17] | 斎藤毅『Fermat予想１(岩波講座 現代数学の展開)』岩波書店, 2000 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [18] | 『数学のたのしみ フェルマー最終定理以後の数論』2000年２月号, pp.25-31, pp.46-97, 日本評論社 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [19] | 数学セミナー編集部『20世紀の予想 現代数学の軌跡』pp.2-11, pp.53-62, pp.91-99, 日本評論社, 2000 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [20] | 『数論の歩み 未解決問題への挑戦 (別冊・数理科学)』サイエンス社, 2000 | |||||||||||||||||||||||||||||||||||||||||||||||||
| [21] | 砂田利一監修『数学の最先端 21世紀への挑戦 volume３』シュプリンガー・フェアラーク東京, pp.166-183, 2003 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| ©Copyright 2024 SAKATA MASAHIRO. All Rights Reserved. | ||||||||||||||||||||||||||||||||||||||||||||||||||